¿Cómo EVALUAR (rutinariamente) la validez de una CURVA de calibración lineal?
"Revisaremos 3 alternativas de evaluación (adicionales al coeficiente de correlación), y algunas herramientas estadísticas que se pueden aplicar"
En la norma ISO/IEC 17025: 2017📄, ítem 7.7.1 se indica:
“El laboratorio debe contar con un procedimiento para hacer el SEGUIMIENTO de la validez de los resultados. Los datos resultantes se deben registrar de manera que las tendencias sean detectables y cuando sea posible, se deben aplicar TÉCNICAS ESTADÍSTICAS para la revisión de los resultados…”
Esta vez nos enfocaremos en las curvas de calibración lineal que se obtienen en los ensayos de análisis instrumental, tales como: HPLC, CG, ICP-OES, PCR, ELISA, etc.
Curva de calibración: Expresión de la relación entre la indicación y el valor de la magnitud medida correspondiente [1].
Para un mejor entendimiento🤓 dividiremos la explicación en 2 etapas:
✅ Estudio de Linealidad del método de ensayo
✅ Seguimiento de la Linealidad en los ensayos de rutina
¡Comencemos! ▶️
1. Estudio de Linealidad del método de ensayo
En el estudio de Linealidad📈, realizada en la verificación o validación del método de ensayo🧪, se define la relación funcional (lineal, cuadrática, etc.) entre la concentración de las soluciones estándar (x) y la señal o respuesta analítica del instrumento (y), tal como se muestra en la imagen para un modelo lineal [2]:
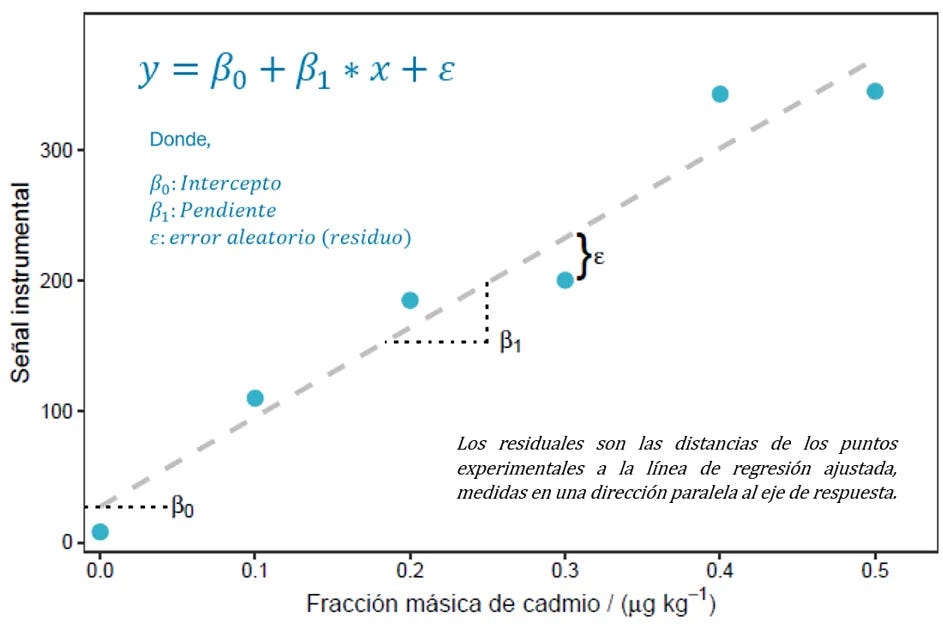
⚠️NOTA 01: “Estrictamente hablando, no podemos probar la linealidad📈 como tal. Lo mejor que podemos lograr es mostrar que una desviación de la linealidad … no es estadísticamente significativa. Un enfoque en este sentido es examinar los residuos de una regresión lineal” [3].
En RESUMEN, los parámetros de regresión lineal (intercepto y pendiente), debido a la presencia de residuos no se pueden conocer, por ello se realizan estimaciones para el intercepto (a) y la pendiente (b) y la ecuación se denota como: y = a + bx. Las estimaciones consideran supuestos asociados a los residuos, tales como: distribución normal, no autocorrelación, etc. Los métodos de estimación más usuales son [2]:
Minimos cuadrados ordinarios (OLS) → residuos homocedásticos (dispersión de residuales aprox. constante en todo el intervalo de concentraciones)
Mínimos cuadrados ponderados (WPS) → residuos heterocedásticos (no se cumple el suspuesto de homocedasticidad)

⚠️NOTA 02: Ignorar esta característica de la mayoría de las calibraciones analíticas puede ocasionar un incremento en el sesgo de la cuantificación de analitos, particularmente en la región de bajas concentraciones [2]
🤔¿Y el coeficiente de correlación📈? …
El coeficiente de correlación (Pearson) es uno de los estadísticos comúnmente utilizados en la evaluación de linealidad. Desafortunadamente, se malinterpreta fácilmente por no considerar lo siguiente[2],[3],[4]:
la correlación y la linealidad solo están vagamente relacionadas. El coeficiente r es una medida de correlación (asociación de variables), no una medida de linealidad (ajuste del modelo);
Un valor r bajo no significa necesariamente que no haya correlación. Podría haber una relación entre los valores “x” i “y”, pero no lineal
Para complementar, revisemos el “Cuarteto de Anscombe”, donde se muestra que un mismo valor de correlación, gráficamente puede representra diferentes situaciones. Por estas razones, es esencial graficar los datos durante la evaluación[3],[7].
⚠️NOTA 03: El objetivo no es desmeritar el uso del coeficiente de correlación, la idea es entender que no podemos utilizarlo como único criterio de aceptación.
✍🏻Por lo tanto, …
El proceso de evaluación de la linealidad puede ser abordado a través de las siguientes estrategias [2]:
Análisis Exploratorio: basado en un análisis de correlación (+gráfico).
Pruebas de significancia: basado en la evaluación del modelo y sus parámetros (pendiente e intercepto).
2. Seguimiento de la Linealidad en los ensayos de rutina
Ahora que ya hemos demostrada la linealidad del proceso de medición, debemos garantizar que esta característica se mantiene en el tiempo en nuestros ensayos🧪 de rutina🗓️.
En las calibraciones analíticas, la función matemática📈 (y = a + bx) se utilizará para obtener los resultados de las muestras (xi=(yi-a)/b), por ello, es importante DEFINIR y VALIDAR los valores a utilizar para la PENDIENTE y el INTERCEPTO [4],[6] … En rutina, es una práctica común evaluar el coeficiente de correlación, y en algunos casos es la única actividad que se realiza (Ver: “Pregunta del día”)… pero; en este punto, ya sabes que ⚠️el coeficiente de correlación no es un criterio suficiente para garantizar la validez de los resultados.
Ahora te presento 3 alternativas que puedes implementar en tu laboratorio:
Coeficientes de variación de los factores de respuesta (f)
Gráficos de control para la pendiente (b) y el intercepto (a)
Uso de estándar control
1️⃣ Coeficientes de variación de los factores de respuesta (f)
📍¿Cómo realizar la evaluación?
El factor de respuesta (f) expresa la relación entre la lectura o respuesta (área) y la concentración [8].
Se calcula f para cada concentración, y con el promedio (p) de los factores de respuesta y su desviación estándar (sd), se obtiene el coeficiente de variación (%CV)[8]:
📍¿Cuál es el criterio de aceptación?
En una calibración lineal los factores de respuesta deben ser semejantes entre si y cercanos al valor de la pendiente. Valores del coeficiente de variación superiores al 5% serían indicativos de una posible falta de linealidad, siendo recomendables valores no superiores al 2% [8].
📍¿Cuál es la desviación que se puede identificar?
El factor de respuesta es una expresión aproximada de la sensibilidad (pendiente) de la curva de calibración en cada punto. Valores del %CV superiores al 5% también pueden reflejar resultados con %recuperación (%eficiencia) por fuera de los límites permitidos.
Ilustraremos 4 casos con diferentes %CV, para un método con los siguientes criterios de aceptación (⚠️Nota: considerar que los cálculos en Excel (pendiente, intercepto) aplican el método de mínimos cuadrados ordinarios)
%Recuperación: 90% al 110% (en este caso, %eficiencia del modelo)
Coef. Correl.: ≥ 0.995
Caso 01🖊️: %CV < 2% → %Eficiencia del modelo conforme
Caso 02🖊️: %CV entre 2% y 5% → %Eficiencia del modelo conforme
Caso 03🖊️: %CV entre 5% y 10% → %Eficiencia del 1er punto NO conforme
Caso 04🖊️: %CV > 10% → %Eficiencia del 1er y 2do punto NO conforme
⚠️NOTA 04: En los casos presentados, el coeficiente de correlación no pudo identificar las desviaciones en los %eficiencia. Estas desviaciones pueden estar relacionadas a efectos sistemáticos (ruido, interferencias → error constante) o un problema en la preparación de las solución estándar.
2️⃣ Gráficos de control para la pendiente (b) y el intercepto (a)
📍¿Cuál es la desviación que se puede identificar?
Primero, es importante conocer la diferencia más resaltante entre los límites de confianza (intervalos de confianza) y los límites de control (gráficos de control) [9]:
Los límites de confianza estiman la incertidumbre de un parámetro (se puede obtener en el análisis de regresión de Excel).
Los límite de control monitorean la estabilidad de un proceso en el tiempo (se puede aplicar la ISO 7870-2).
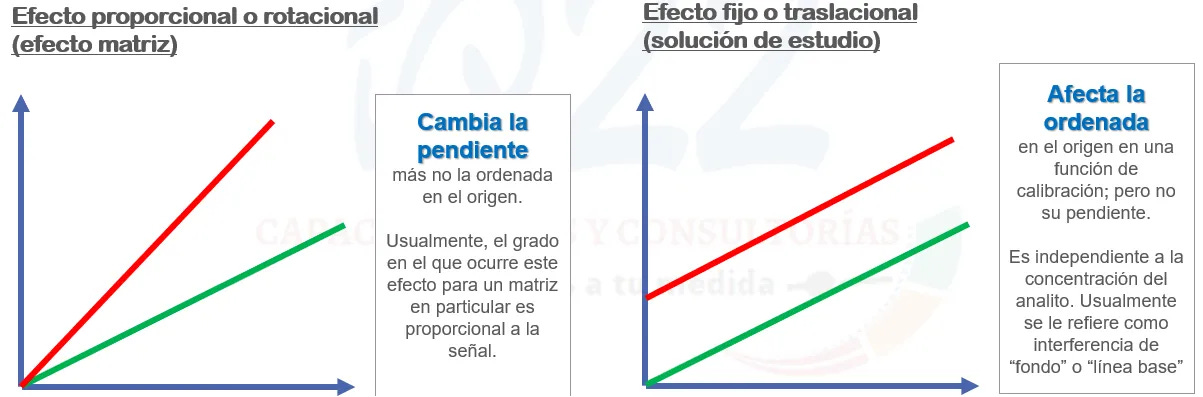
En este caso, trabajaremos con las gráficas de control para identificar desviaciones significativas en la pendiente y el intercepto en el tiempo [11], ya que pueden generar un error en el cálculo de resultados. En la siguiente gráfica se muestra como podrían cambiar la pendiente y el intercepto sin afectar la linealidad del proceso y el coeficiente de correlación tampoco podría identificar estas desviaciones.
📍¿Cómo realizar la evaluación? y ¿Cuál es el criterio de aceptación?
La ISO 7870-2. Control Charts - Shewhart control charts, se dan detalles para la elaboración y seguimiento de las gráficas de control… Para la toma de datos se recomienda lo siguiente [5],[8]:
Uso en paralelo de un MR de concentración conocida,
Ejecución del ensayos por el analista de mayor experiencia,
Preparación de cada curva de calibración de manera indepediente desde la preparación de la solución stock y, de ser posible, evitar las diluciones sucesivas para eliminar errores sistemáticos que se puedan derivar de una mala preparación de la solución stock,
Trabajo en condiciones de precisión intermedia (similar condiciones rutinarias).
3️⃣Uso de estándar control
📍¿Cuál es la desviación que se puede identificar?
Al ser un estándar de concentración conocida, un resultado no conforme puede reflejar los siguientes problemas en las curvas de calibración:
Error en la preparación
Inestabilidad (fecha de caducidad)
Impurezas (contaminación o grado de pureza)
📍¿Cómo realizar la evaluación? y ¿Cuál es el criterio de aceptación?
En la preparación, si se utiliza el mismo producto químico, o peor aún, la misma solución madre, para la calibración y el control, ⚠️los errores pueden camuflarse, por ello se pueden utilizar productos de diferentes proveedores o diferentes lotes[11].
Generalmente el estándar control se analiza al inicio del proceso para asegurar que la calibración es correcta[12], también se pueden analizar al intermedio o al final para evaluar la estabilidad en el tiempo que dura el ensayo[6].
Se puede elaborar una gráfica de control en base al valor medio del estándar. En algunos casos se utiliza como criterio de aceptación que el %recuperación esté dentro del rango permisible para el método.
¿Ya aplicas estos controles? o ¿Que otros controles recomiendas aplicar?
¿Deseas conocer nuestros cursos taller vigentes?🧑💻: Revisar Aquí
Referencias bibliográficas
[1] IUPAC (2021). Metrological and quality concepts in analytical chemistry
[2] INM (2023). Validación de métodos en análisis químico cuantitativo
[3] AMC (2006). Is my calibration linear?
[4] LGC (2003). Preparation of Calibration Curves. A Guide to Best Practice
[5] ISO 11095 (1996). Linear calibration using reference materials
[6] EURACHEM (2016). La Adecuación al Uso de los Métodos Analíticos
[7] Anscombe, F. (1973). Graphs in Statistical Analysis
[8] AEFI (2001). Validación de métodos analíticos
[9] Miller, J. and others (2018). Statistics and Chemometrics for Analytical Chemistry
[10] ISO 7870-2 (2023). Control charts - Shewhart control charts
[11] NORDTEST NT TR 569 (2018). Internal Quality Control
[12] AMC (2010). Internal quality control in routine analysis







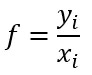






Excelente publicación, Julissa